increpare games

Where I do add another journalistic account of a tribe I visited before, that had a system of unordered counting quite remarkable.

I came across a village some forty days south of where I met that tribe tribe whose inhabitants were, astoundingly, even more puritanical in their approach to counting – or rather to assigning cardinalities.

These people had accepted the arts of reading and arithmetic into their culture with great success but, when I told them of the nomadic tribe from the previous article, they broke into laughter at the very naivety of the idea!

This had me taken aback – not only had they seemed to have completely comprehended what I had told them, but they had simultaneously judged the idea to be worthless, or so I thought. When I asked them to explain themselves, I learned that such ideas had reached them long ago, and that they had advanced such trains of thought far further than the northerners I had thought so exceptional.

The most respected of the village elders, over evening meal, explained to me their philosophy of counting. He made clear that they did not ridicule the notion of an unordered set in and of itself, but rather of a large unordered set. He declared fully that unordered sets could only consist of either one, two, or three items and that indeed the only numbers were one, two, and three.

Immediately after stating this, I inquired if he did believe in the empty set. He shrugged nonchalantly; such matters did not seems to prick at his philosophical conscience much as it did those of us in the Western world. I then asked him to explain his rather grandiose claim.

He came to sit closer to me and asked how many colours were there, essentially. I replied that there were three: red green and blue. He asked me if I thought there to be any fundamentally important relationships amongst those three colours, if I thought any larger or more important than any other, if there was any ordering to them, and I replied that I did not.

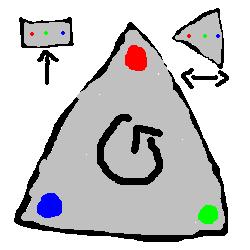
He went over to fetch a small box containing coloured chalk, and a perfectly smooth & symmetrical triangular piece of slate, asking me to draw them on the slate.

I picked three pieces of chalk and drew three small circles in a row, red green and blue, forming a line from one of the corners down the middle of the triangle to side opposite.

He asked me why I did put red on the small side and blue on the large side. I said that I had no reason for doing so. He said then, that if I had a slate that was instead a rectangle, that the information I sought to communicate, namely the three colours, might come across more clearly if there were no ways of distinguishing the colour on one side from the colour on the other.

On the triangular slate, if picked up, one could be told to hold the slate so that the line was horizontal, and that the pointed side was facing left, and so be able to talk in some way of a “left” and “right” colour, but one could not be given such commands if there was no way of distinguishing left from right on the slate. I thought that a curious idea, but there was some reasoning to it, so I said yes.

He then asked me why I did put green in the middle. I said that I had no reason, but that one always had to put some colour in the middle if one was drawing three colours in a row. He said that he did not find such arrangements satisfactory. He said, if there is no meaning to the middle, then why should one have a middle at all? I thought about this – clearly, the fact that green was in the middle couldn’t be remedied by changing the shape of the tile.

I asked him then what he proposed be done about it. He took the slate from me, rubbed out the three colours, and put them on the slate again himself, but this time there was one at each edge. Now there was no colour on the inside, and no colour to the left or right of any colour. But then something came to my mind.

“Is not green located counterclockwise from red?” I asked.

He smiled warmly. “Yes,” he said “there is still a problem here. There is no way to talk about three on the side of a slate or parchment”.

“But one can display sets of size two to your satisfaction?” I asked – he nodded.

I was still puzzled. “So why, then, do you still believe that three is a number?”

He grinned at me; “Thankfully, we do not live on the sides of slates or scrolls”. He turned around the slate, and drew the three colours by each of the edges, with the colours back to back matching.

“Now,” he said, pointing to the other side, “green is located clockwise from red on this other side – now no sense of chirality can be used to evince any patterns from this arrangement, nor indeed is there any way at all to”.

“And”, he added, “one cannot produce any patterns to display any larger sets where there are no interrelations. This is why I say that the only numbers are one, two, and three: any larger collection simply must, by the geometry of this universe, have some structure to it’s contents rendering it undescribable by a mere number. Of course, not every collection of size three has no internal structure, but it is a physical impossibility that there be any collection of size greater than three with no internal structure”.

Then I responded “just because one cannot represent such things geometrically, that does not mean that they do not exist”.

He laughed at what he perceived to be the dim-wittedness of my suggestion.