Simple ball probability problem

Problem

Given a circular table, place one small ball in the centre of the table and another ball of equal radius to the first at a random position. If the centre ball is hit in a random direction, what is the chance that it will hit the other ball (once it reaches the edge of the table it falls off)?

Solution

Part 1

Call the radius length of the balls r, and call the radius of the table R.

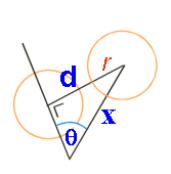
Given that the randomly placed ball is at a distance x from the centre, what’s the chance that it will be hit by the other ball? The other ball will hit it if the minimal distance between that ball and the path of the other ball is less than 2r.

But from the diagram below d = x sin θ.

diagram relating d x and θ

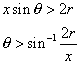
x sin θ > 2r

But this only accounts for θ on one side, and so because either side of the ball can be hit either side, the total number of radians in which the colliding ball can be launched is .

And so the probability that the ball will take one of these angles as opposed to any other is

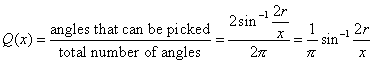
1/π arcsin(2r/x)

Part 2

Let P(p<x) denote the chance of a point placed at random of a disk of radius
R will be found within a distance x of the centre of the circle.

Obviously

P(p< = R) =1 and P(p=0) = 0

And a simple approximation of the probability can be given in terms of the ratio of areas:

However, if there is a ball of radius r placed in the centre of the disk, the other ball will not be able to have a centre closer than 2r to the centre, so we must adjust the probability, first by truncating the probabilities below 2r, then by scaling the remaining ones so that they add up to 1.

So let , and
let’s try and calculate k and c:

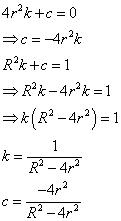
rewriting things to find k and c

Which gives the probability

Part 3

To combine the two above probabilities, we find the probability that a point will lie on between two different radii, x and x+Δx.

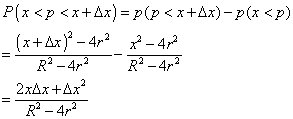
simplifying P(x < p)

Getting the limit to find the probability that the point will lie on a certain radius (as a differential of course).

Now, the chance that a ball will be found on a given radius times the chance that a ball will hit is given by the multiple of the above formula by the formula in part 1.

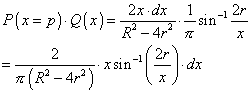
big equation for P(x=p).Q(x)

Integrate this over the radii where the centre of the second ball can be found to get the probability that the centre ball will hit the other ball.

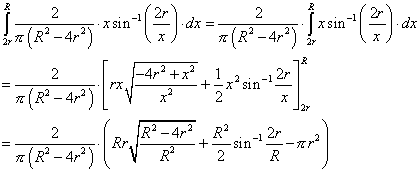
another big equation for the integral of
the previous equation

This is the probability that on a given table of radius R, that the ball launched from the centre will hit another randomly placed ball (both of radius r).

Of course, no generality will be lost if instead of R and r we use their ratio (The probabilities do not change. If any proof is needed of this the following substitution should suffice)

Letting , we get the probability as being

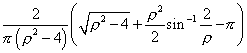
big equation

And, when graphing the ratio (x-axis) against the probability (y-axis), you get the following distribution (courtesy of gnuplot):

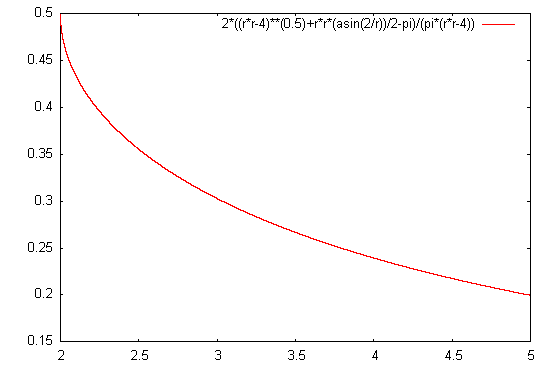
graph

With the limit as the ratio approaches 2 being 0.5 (by l’Hopital’s rule).

(I thought I had this all wrong until I realized that 1/2 in gnuplot is thought of as integral division and evaluated as 0, and so until I entered 0.5 a few minutes ago in desperation as the square root power I had a seriously fucked up graph, and was about to give up hope of ever figuring out Newtonian calculus).

And another graph just for the heck of it:

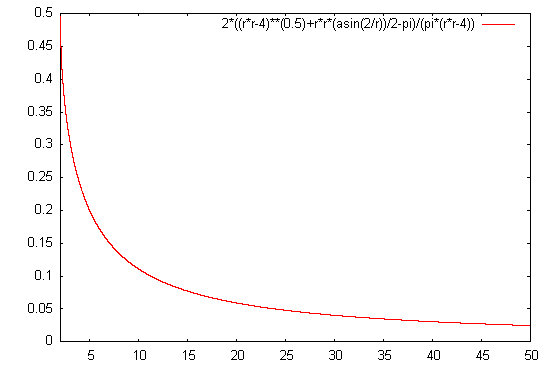
another graph.

Ok, enough of gnuplot for me, I’m off to buy a super-expensive graphing calculator that knows only of real numbers (unnoticed integral division, I spit on your corpse! Hah!).

increpare games